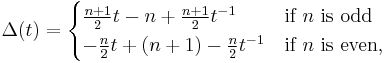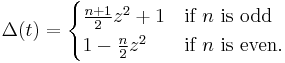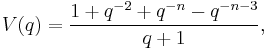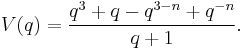Twist knot

In knot theory, a branch of mathematics, a twist knot is a knot obtained by repeatedly twisting a closed loop and then linking the ends together. (That is, a twist knot is any Whitehead double of an unknot.) The twist knots are an infinite family of knots, and are considered the simplest type of knots after the torus knots.

Contents

Construction

A twist knot is obtained by linking together the two ends of a twisted loop. Any number of half-twists may be introduced into the loop before linking, resulting in an infinite family of possibilities. The following figures show the first few twist knots:

Properties

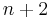All twist knots have unknotting number one, since the knot can be untied by unlinking the two ends. Every twist knot is also a 2-bridge knot.[1] Of the twist knots, only the unknot and the stevedore knot are slice knots.[2] A twist knot with n half-twists has crossing number n%2B2. All twist knots are invertible, but the only amphichiral twist knots are the unknot and the figure-eight knot.

Invariants

The invariants of a twist knot depend on the number n of half-twists. The Alexander polynomial of a twist knot is given by the formula

\Delta(t) = \begin{cases} \frac{n%2B1}{2}t - n %2B \frac{n%2B1}{2}t^{-1} & \text{if }n\text{ is odd} \\ -\frac{n}{2}t %2B (n%2B1) - \frac{n}{2}t^{-1} & \text{if }n\text{ is even,} \\ \end{cases}

and the Conway polynomial is

\Delta(t) = \begin{cases} \frac{n%2B1}{2}z^2 %2B 1 & \text{if }n\text{ is odd} \\ 1 - \frac{n}{2}z^2 & \text{if }n\text{ is even.} \\ \end{cases}

When n is odd, the Jones polynomial is

V(q) = \frac{1 %2B q^{-2} %2B q^{-n} - q^{-n-3}}{q%2B1},

and when n is even, it is

V(q) = \frac{q^3 %2B q - q^{3-n} %2B q^{-n}}{q%2B1}.

References

  1. ^ Rolfsen, Dale (2003). Knots and links. Providence, R.I: AMS Chelsea Pub. pp. 114. ISBN 0-8218-3436-3. 
  2. ^ Weisstein, Eric W., "Twist Knot" from MathWorld.